Правила решения какуро

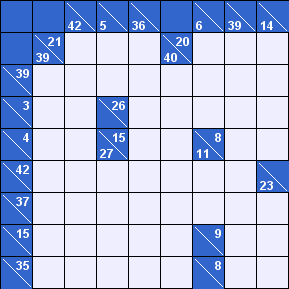Условия головоломки: вам нужно заполнить поле цифрами от 1 до 9 так, чтобы получить суммы, указанные в клетках сверху (сумма по вертикали) и слева (сумма по горизонтали). Суммирующиеся цифры уникальны и не могут повторяться.
Решение основано на том, что для каждой суммы и для каждого количества клеток, из которых составляется эта сумма, существует достаточно ограниченный набор вариантов цифр, дающих нужную сумму. Например, сумма [4] из двух клеток означает, что в этих клетках – цифры 1 и 3. Сумма [23] из трех клеток – 6+8+9. Сумма [5] из двух клеток – либо 1+4, либо 2+3. И так далее. При разгадывании вы можете навести курсор мыши на сумму, чтобы получить подсказку по вариантам.

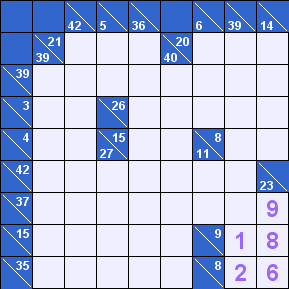Начнем решение с правого нижнего угла. Здесь «пересекаются» суммы: [23] по вертикали с [8] и [9] по горизонтали. Как мы уже говорили, [23]=6+8+9, и других сочетаний быть не может. Нам нужно только определить, в какой клетке стоит каждая из этих цифр.
Логично, что в сумму [8] не может входить ни 8, ни 9. Так что в нижней клетке – 6. Аналогично, для суммы [9] из оставшихся цифр подходит только 8, значит, 9 – в верхней клетке.
Проставив цифры, простой арифметикой находим вторые слагаемые для сумм – [8]-6=2 и [9]-8=1.

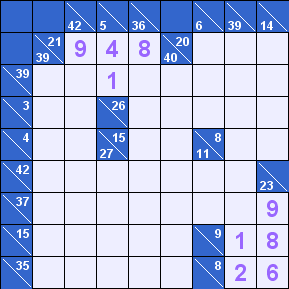Переходим в верхний левый угол, на пересечение [21] с [42], [5] и [36]. У [21] несколько вариантов расклада цифр, но ни в одном из них нет цифр меньше 4. В сумме [5] же, как мы понимаем, не может быть цифр больше 4. Так что 4 – единственная цифра, которая может стоять на этом пересечении.
Единственный вариант [21] с «четверкой» – [21]=4+8+9. Анализируя варианты для [36], обнаруживаем, что 9 там быть не может, значит, на этом пересечении – 8, а в оставшейся клетке – 9.
Не забываем [5]-4=1.

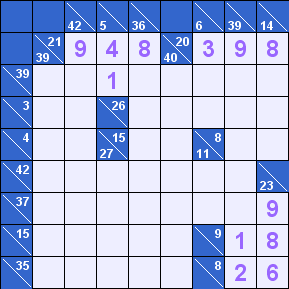На очереди верхний правый угол, пересечение [20] с [6], [39] и [14].
Точно так же, как и в предыдущем случае, находим единственную цифру, подходящую для пересечения [20] и [6] – 3. Получаем вариант [20]=3+8+9 и находим, что в [14] не может быть 9, только 8.

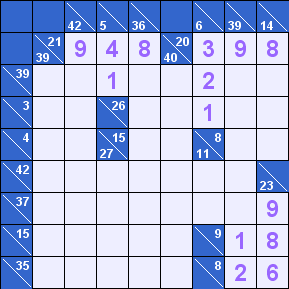Та же сумма [6] раскладывается на [6]=1+2+3. «Тройку» мы уже поставили, нужно определить порядок двух других цифр. Мы видим, что «единица» должна быть в нижней клетке, так как средняя клетка принадлежит горизонтальной группе, в которой такая цифра уже есть. Важно: правила какуро не запрещают повтор цифр по горизонтали и вертикали, но только в том случае, если эти цифры не принадлежат одной суммирующейся группе.

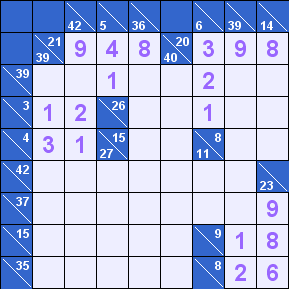Мы тут же видим подтверждение этого правила – «единица» обязательно должна быть в сумме [3]=1+2. Соседняя сумма имеет единственный вариант [4]=1+3. Обе эти суммы пересекаются с [42]=1+2+4+5+6+7+8+9, в которой «тройки» нет. Так мы определяем порядок цифр в [4], а «единица» в [3], естественно, должна располагаться на другой вертикали.

Начинающим желательно потренироваться на низком уровне сложности (у этого примера – высший). Решение пойдет легче, если вы запомните ключевые суммы, на которые надо обращать внимание в первую очередь.
«Двухклеточные»: [3]=1+2, [4]=1+3, [16]=7+9, [17]=8+9.
«Трехклеточные»: [6]=1+2+3, [7]=1+2+4, [23]=6+8+9, [24]=7+8+9.
И так далее.